Grade 3 Maths (imo): Fractions

The numbers in a fraction are called the numerator, on the top, and the denominator, on the bottom. ^numerator/_denominator
Proper fractions have a numerator smaller than the denominator.
Examples include ¹/₂, ³/₄ and ⁷/₈.
Improper fractions have a numerator larger than the denominator.
Examples include ⁵/₄, ³/₂ and ¹⁰¹/₇.

Grade 3 Maths (IMO) : Number sense

Face value of a digit is the digit itself whereas Place value can be termed as the location of the digit in the numeral.

The value of a place in the place value chart is 10 times the value of the place just to its right.

A quick look at the grade 2 lesson on introduction to multiplication

An even number x an even number = an even number

An odd number x an even number = an even number

An odd number x an odd number = an odd number

Listing down some methods to simplyfy addition.

Doubles (such as 6 + 6)
Near doubles: Try adding a double and the remainder. Solve 7 + 6, (6 + 6+ 1) or (7 + 7 – 1).
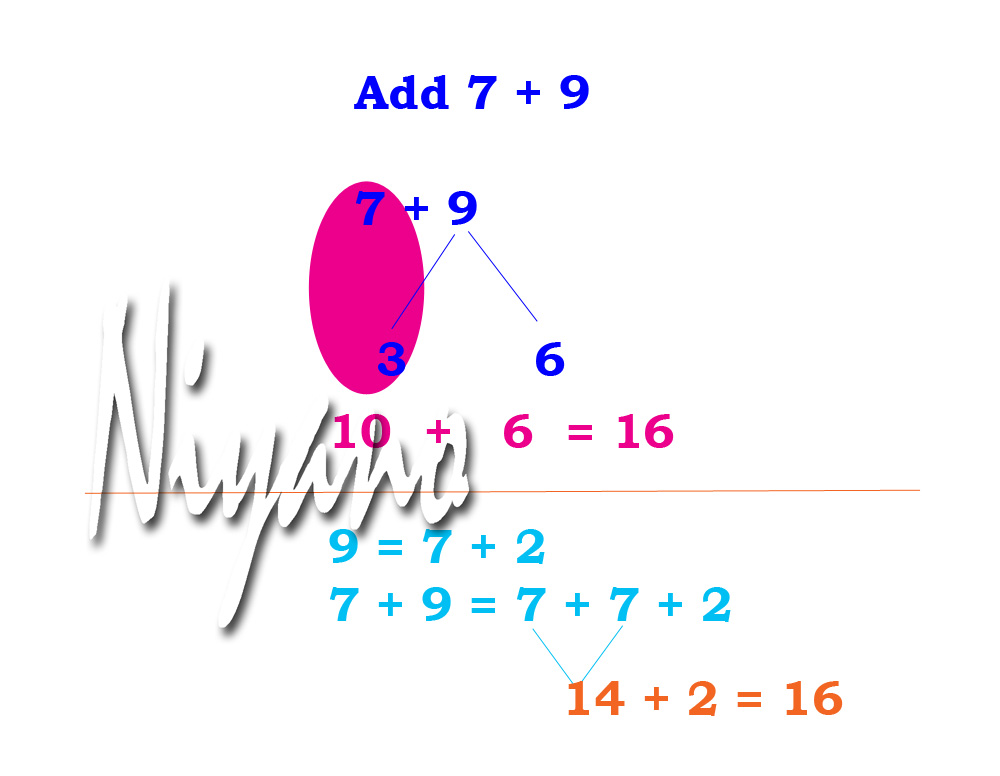
Making a ten or a multiple of 10: To add 7 + 6, I can take 3 from the 6 and put it with the 7 to make 10 and 3. This holds good even with multiples of 10 like 20, 30 40, etc
1 more, 1 less: Show problems such as: 8 + 1, 51 + 1, and 6 – 1, 22-1
Place value Decomposition: 35 + 22 can be decomposed into tens and ones 30+20 added to 5+2. Or 35 – 22 can be decomposed to 30-20 plus 5-2.

Pictorial representation of the strategies above :