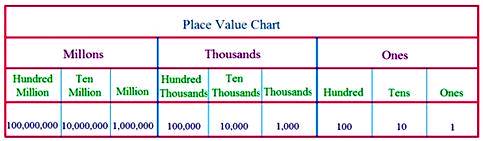
Balance as a model of an equation

This article discusses how to use a balance to model simple linear equations in pre-algebra or algebra 1. On this page, we only deal with positive integers;

An equation is basically saying that two things (expressions, to be exact) are EQUAL. Since in a balanced situation the two sides of the balance hold equal weight, we can model simple equations with a balance.

In the pictures below, each circle represents one and the block represents the unknown x. To find out what the block weighs, you can

• add the same amount (circles or blocks) to BOTH sides
• take away the same amount from BOTH sides

That way both sides will maintain the balance or “the equality”.

3x + 2 = 2x + 6	Take away two blocks (two x‘s) from both sides. The balance will stay balanced.
x + 2 = 6	Take away 2 circles from both sides.The balance will stay balanced.
x = 4	Here is the solution!

Without the scale model, the solving process looks like this:

3x + 2 -2x	=	2x + 6 -2x		(take away 2x from both sides)
x + 2 -2	=	6 -2		(take away 2 from both sides)
x	=	4

Dividing

In some situations you have to divide both sides of the equation by the same number.  When is that? It’s in the fortunate situation where there are ONLY x’s (blocks) on one side but there are more than one.

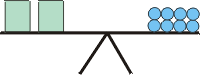
2x = 8	If you take away half of the things on the left side, and similarly half of the things on the right side, the balance will stay balanced.
x = 4

3x = 9	Think about it! If one is a balanced situation…
x = 3	…so is the other (and vice versa)! We simply divided both sides by 3.

Combining the operations

The allowed operations are:

• Add the same amount to both sides (either x‘s or ones)
• Subtract the same amount from both sides (either x‘s or ones)
• Multiply both sides by the same number (but not by zero)
• Divide both sides by the same number (but not by zero)

(There are others, too, but they are not needed in simple equations.)

The goal is to FIRST add and subtract until we have ONLY x‘s (blocks) on one side and ONLY ones (circles) on the other. Then, if you have more than one block, you need to divide so as to arrive to the situation with only one block on the one side, which is the solved equation!

Multiplying both sides can occur if you have a fractional block (less than one block) on one side. For example, the equation  1/4x = 13  is solved by multiplying both sides by 4.  Try let your students model the equation 1/2x + 14 = 20 using a balance; they can solve it with it. More advanced students can ponder what to do about the equation 2/3x = 12.

Example of both subtracting and dividing

In this example we use all the abovementioned operations: taking away from both sides of the equation and dividing the equation by the same number.

4x + 2 = 2x + 5First we get rid of the blocks on the right side by taking away two blocks from both sides.

2x + 2 = 5Then we eliminate the circles on the left side by removing 2 circles from both sides.

2x = 3Now there are only blocks on one side and only circles on the other. To find out what 1 block weighs, we take half of both sides.

x = 1 1/2The solution is that 1 block weighs 1 1/2 circles.

Try substituting this value x = 1 1/2 into the original equation 4x + 2 = 2x + 5 and check if the equation becomes true!

Example exercises

These equations are simple enough that you can solve them using a balance model. ALWAYS check your solution by substituting it into the original equation.

1. 2x + 3 = 5
2. 2x + 5 = x + 9
3. 3x + 2 = 2x + 4
4. 3x + 3 = 5 + x
5. 5x + 4 = 3x + 6
6. 6x + 2 = 3x + 6
7. 6x + 3 = 2x + 5

Let’s talk about what division really is — it is repeated subtraction; much the way multiplication is repeated addition.

Let’s say I have the basic problem 16 ÷  4.  I could start with 16 and then subtract 4, subtract another 4, another 4, and another 4 until I run out and reach zero.  I would have to do this 4 times. If I had 16 cookies that I wanted to share equally among 4 friends, I could do the “one for you, one for you, one for you, and one for you” process and still end up with 4 cookies for each.

But what about 375 ÷ 50? If I don’t know how to divide by double digit numbers, the repeated subtraction process might actually be a good choice . . . at least showing some number sense to know that 375 divided by 50 means “How many 50’s in 375?” I know if I subtract 50 six times, I still have 75 left. I can subtract another 50 and I have 25 left over. So 375 ÷ 50 = 7 with a remainder of 25.

Dividing using the distributive law

 Long Division

Before a child is ready to learn long division, he/she has to know: Continue reading →